A verdade sobre o anatocismo
Por: Newton Bandeira de Mello Golek
Ao longo dos 12 anos em que atuo como Perito Judicial na área Econômico-Financeira, especificamente quando o assunto é referente à capitalização dos juros pelos bancos, tenho observado que um determinado número de “profissionais” que se apresentam como “Peritos”, afirmam categoricamente que as referidas instituições não capitalizam os juros (incluindo a Tabela Price) e que portanto não há anatocismo. E, além de se apoiarem em legislações, súmulas para justificar o injustificável, distorcem a verdade, através da canibalização da matemática financeira. Tal fato, além de preocupante é alarmante, tendo em vista que tais afirmações, além de faltarem com a verdade, comprometem as decisões judiciais.
Em virtude disso, tendo em vista que na literatura da matemática financeira não existem leis jurídicas e sim fórmulas e conceitos sobre juros simples e juros compostos, decidi de uma ver por todas, com base na minha formação e em meus contínuos estudos, por fim à esta discussão desnecessária, apresentando a verdade sobre o assunto, para que a discussão saia de vez do campo da matemática e fique no campo jurídico, já que, ao contrário da matemática, o Direito não é uma ciência exata.
Apresentarei todas as provas matemáticas por etapas, para que de uma vez por todas, após este esclarecimento, o assunto seja encerrado.
1- Conceitos de Juros Simples e Juros Compostos
1.1- Juros Simples (Capitalização Simples ou Linear)
São os juros os quais o investidor, no período T, recebe juros sobre o capital investido originalmente, ou seja, são os juros aplicados sobre o capital original.
Em cada período, o investidor recebe o valor iC de modo que após n períodos o seu saldo passa a ser:
FV= PV(1+i)n
Onde:
FV=Valor Futuro
PV= Valor Presente
i=taxa
n= prazo
Exemplo:
Qual é o valor de um Montante (Capital + juro) a 10% a.m. no prazo de 12 meses, sendo que o capital aplicado seria de
R$ 1.000,00?
Solução: Aplicando-se a fórmula acima, obteríamos o valor de R$ 2.200,00, conforme abaixo demonstrado:
FV =?
PV= R$ 1.000,00
I = 10 %
n= 12
FV= R$ 1.000,00 x (1+0,1×12)
FV =R$ 1.000,00 x 2,2
FV= R$ 2.200,00
Se observarmos, veremos que, sob a ótica da matemática pura, estamos diante de uma equação de primeiro grau ou equação linear conforme abaixo:
y = ax+b onde:
a=100
x= tempo.
B= 1000
Y= 100x+1000
Se aplicarmos a nomenclatura da matemática financeira, seria:
Y= 100x (tempo)+ 1000 (capital).
Assim seria a evolução do saldo, conforme quadro abaixo:
REGIME DE CAPITALIZAÇÃO SIMPLES
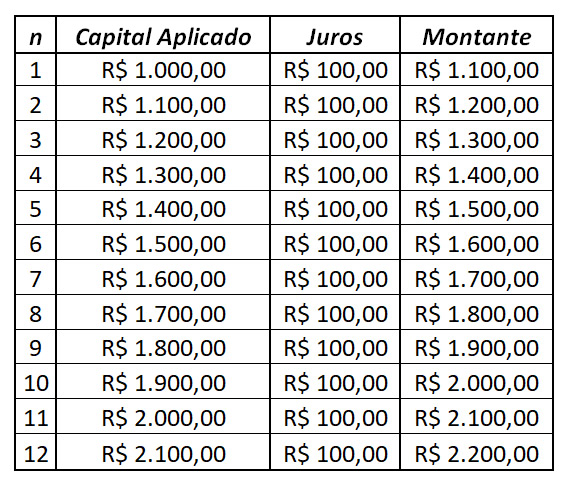
Observa-se que o saldo devedor cresce de uma forma linear, ou seja, R$ 100,00 por mês, formando uma Progressão Aritmética de razão 100, conforme também demonstrado na equação linear “ Y= 100x+1000”.
1.2- Juros Compostos (Capitalização Composta ou Exponencial)
São os juros os quais o investidor, no período T, recebe juros sobre o capital investido originalmente e ainda todos os juros acumulados nos períodos anteriores. Ou seja, são os juros que são cobrados sobre o saldo devedor anterior num determinado período de tempo.
No caso de juros compostos, o lucro do investimento não depende do capital investido, mas apenas a taxa de juros i e do prazo total n.
Seria representado pela equação:
FV = PV (1+i)n
Exemplo:
Qual é o valor de um Montante (Capital + juro) a 10% a.m. no prazo de 12 meses, sendo que o capital aplicado seria de R$ 1.000,00?
Solução: Aplicando-se a fórmula acima, obteríamos o valor de R$ 3.138,43, conforme abaixo demonstrado:
FV =?
PV= R$ 1.000,00
I = 10 %
n= 12
FV= R$ 1.000,00 x (1+0,1)12
FV =R$ 1.000,00 x 3,13843
FV= R$3.138,43
Se observarmos, veremos que, sob a ótica da matemática pura, estamos diante de uma função exponencial, conforme abaixo:
Y= 1000e0,0953x
Como se vê, a equação acima, sendo uma função exponencial, comprova a capitalização compostas dos juros.
Assim seria a evolução do saldo, conforme quadro abaixo:
REGIME DE CAPITALIZAÇÃO COMPOSTA
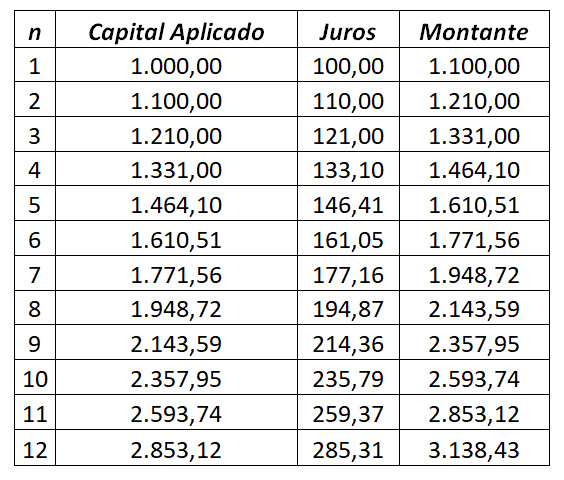
Observa-se que o saldo devedor cresce de uma forma exponencial, ou seja, a cada mês, os juros são cobrados sobre o saldo devedor anterior e o mesmo evolui formando uma Progressão Geométrica , conforme também demonstrado na equação exponencial Y= 1000e0,0953x
COMPARAÇÃO GRÁFICA ENTRE
JUROS SIMPLES E JUROS COMPOSTOS
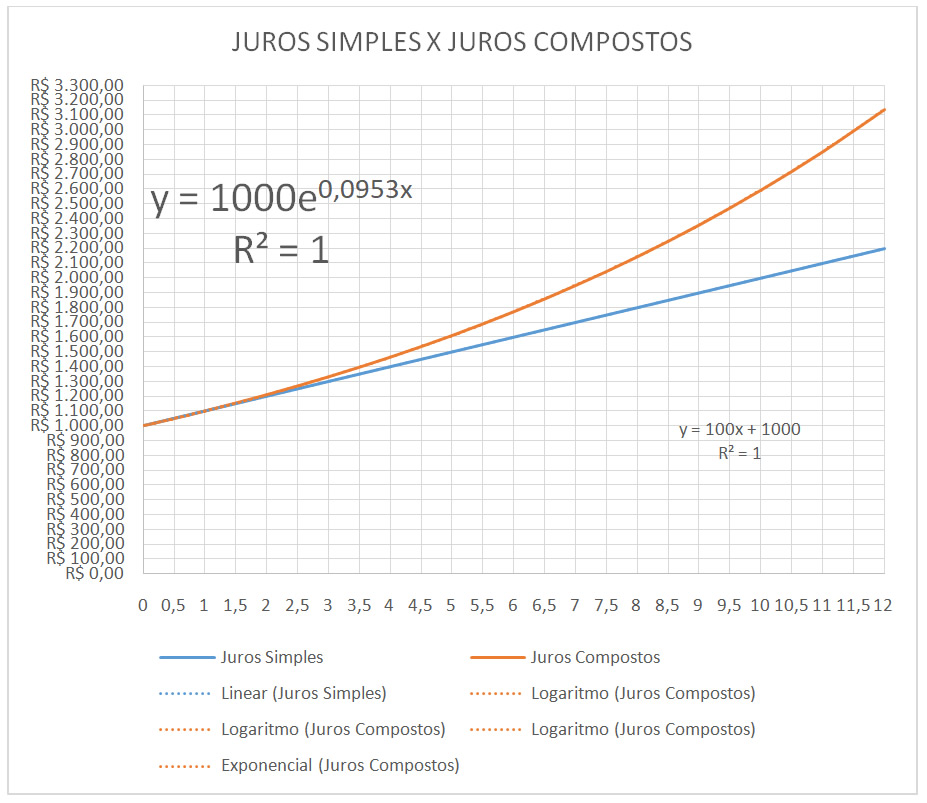
OBSERVAÇÃO
Nota-se que no tempo 1, os gráficos se sobrepõem, atingindo o mesmo valor.
Esse é o único caso em que no tempo 1, a remuneração do capital por Juros Compostos é a mesma dos Juros Simples.
2 . Um breve comentário sobre Richard Price
Nascido na Inglaterra, em 23 de Fevereiro de 1723, após anos de estudos, criou o método utilizado no sistema de pagamentos periódicos com direito à remuneração em benefícios.
Confeccionou então a fórmula que produz a recuperação do Capital a “Juro Composto” que é a mesma coisa que “juro sobre juro” pelo sistema de pagamentos parcelados.
Ou seja, ele mesmo afirma e confessa que suas próprias são baseadas em juros compostos, o que já constitui uma prova irrefutável que a Tabela Price capitaliza os juros da forma composta.
E para complementar ele afirma que “ um centavo de libra emprestado na data de nascimento de nosso Salvador a 5 por cento, juro composto, teria aumentado, no presente ano de 1781, para um valor maior do que o contido DUAS CENTENAS DE MILHÕES de terras , todas de ouro maciço”..
…”Porém, se emprestado a juro simples, teria resultado, no mesmo tempo, num montante nada maior do que SETE XELINS E SEIS CENTAVOS”
O que ele quis demonstrar é que “ o regime de juros compostos quebra qualquer um”.
Portanto senhores Magistrados, não há como negar, diante das provas matemáticas apresentadas, que a Tabela Price capitalizam os juros da forma composta.
Esse artigo, conforme dito no início, tem por objetivo esclarecer de vez, através da matemática, que a Tabela Price capitaliza sim os juros da forma composta.
Observem que nenhuma Súmula ou jurisprudência foi citada, tendo em vista que na literatura da matemática financeira não há leis jurídicas e sim fórmulas e conceitos de juros simples e juros compostos.
NEWTON BANDEIRA DE MELLO GOLEK
PERITO JUDICIAL
CORECON Nº 13.085
Referências:
TABELA PRICE MITOS E PARADIGMAS
SALDO CAPITALIZÁVEL E SALDO NÃO CAPITALIZÁVEL:
NOVOS ALGORITMOS PARA O REGIME DE JUROS SIMPLES























Deixe um comentário